INMULTIREA SI IMPARTIREA NUMERELOR INTREGI
INMULTIREA NUMERELOR INTREGI
Ca si la adunare, si aici avem 3 cazuri, in functie de numerele pe care vrem sa le inmultim.
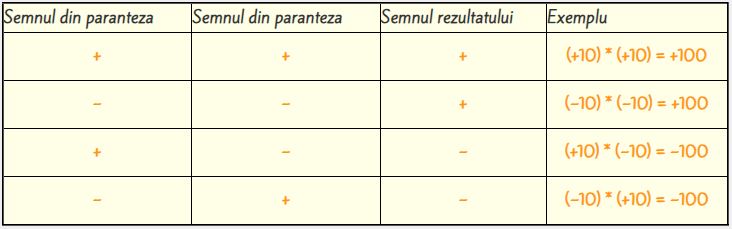
- Inmultirea a doua numere intregi pozitive: se inmultesc direct numerele, iar semnul rezultatului va fi "+". Exemplu: (+5) * (+3) = +(5 * 3) = +15
- Inmultirea a doua numere intregi negative: se inmultesc direct numerele, iar semnul rezultatului va fi "+". Exemplu: (-5) * (-3) = +(5 * 3) = +15
- Inmultirea a doua numere intregi, dintre care unul pozitiv si unul negativ: se inmultesc direct numerele, iar semnul rezultatului va fi "-". Exemplu: (-5) * (+3) = - (5 * 3) = -15
In cazul in care vrem sa inmultim mai multe numere intregi pozitive, rezultatul va fi un numar pozitiv si vom face direct inmultirea numerelor.
Exemplu: (+3) * (+2) * (+5) = + (3 * 2 * 5) = + 30
In cazul in care vrem sa inmultim mai multe numere intregi negative, in functie de cate numere inmultim (adica daca avem un numar par de numere de inmultit sau un numar impar), rezultatul va fi un numar pozitiv - daca avem un numar par de numere de inmultit, respectiv un numar negativ, daca avem un numar impar de numere de inmultit.
Exemplu:
Inmultim un numar impar de numere, adica 3 numere in cazul nostru: (-3) * (-2) * (-5) = + (3 * 2) * (-5) = (+6) * (-5) = - (6 * 5) = -30
Inmultim un numar par de numere, adica 4 numere in cazul nostru: (-3) * (-2) * (-5) * (-2) = + (3 * 2) * (-5) * (-2) = (+6) * (-5) * (-2) = - (6 * 5) * (-2) = (-30) * (-2) = + (30 * 2) = +60
In cazul in care vrem sa inmultim mai multe numere intregi, atat pozitive cat si negative, rezultatul va avea semnul care apare cel mai des la numerele de inmultit, iar numerele se vor inmulti direct.
Exemplu: (-2) * (+3) * (-1) * (-4) * (+10).
Observam ca semnul cel mai des intalnit este "-", acesta aparand la 3 numere (-2), (-1) si (-4), in timp ce semnul "+" apare doar de 2 ori, la numerele (+3), (+10).
Deci, rezultatul va avea semnul "-".
(-2) * (+3) * (-1) * (-4) * (+10) = - (2 * 3 * 1 * 4 * 10) = -240
PROPRIETATI ALE INMULTIRII NUMERELOR INTREGI
- COMUTATIVITATEA: a * b = b * a, pentru orice a, b ∈ Z
- ASOCIATIVITATEA: a * (b * c) = (a * b) * c, pentru orice a, b, c ∈ Z
- ELEMENTUL NEUTRU: a * 1 = 1 * a = a, pentru orice a ∈ Z; 1 este elementul neutru al inmultirii
- DISTRIBUTIVITATEA INMULTIRII FATA DE ADUNARE SAU SCADERE:
- a * (b + c) = a * b + a * c
- a * (b - c) = a * b - a * c
IMPARTIREA NUMERELOR INTREGI
Asa cum stim de la impartirea numerelor naturale, a imparti un numar a la b inseamna a gasi un numar intreg c, numit cat, astfel incat a = b * c.
In cazul numerelor intregi, impartirea se face la fel, iar semnul rezultatului se va aplica ca la inmultire, adica:
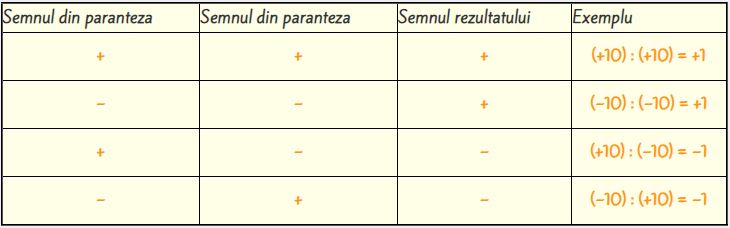
a : 0 nu are sens, oricare ar fi a ∈ Z.
Exemple:
1) a : (-25) = 2
a = 2 * (-25)
a = -50
2) 121 : b = 11
b = 121 : 11
b = 11
3) (-16) : c = (-2)
c = (-16) : (-2)
c = + 8
4) |-31 + 10| : |-3 + 6|
= |-21| : |+3|
= 21 : 3
= 7
